3.1 Les caractéristiques physiques d’une onde sonore

 

L’onde sonore  est caractérisée par plusieurs grandeurs physiques que nous détaillerons dans cette première partie.  Une différenciation entre deux types de signaux sonores se fait : le signal d’un son complexe et le signal d’un son pur. Le son pur est modélisé par une fonction sinusoïdale périodique, cette fonction traduit plusieurs grandeurs qui caractérisent l’onde sonore :

-          une fréquence,

-          une longueur d’onde,

-          une amplitude ou intensité sonore,

-          la durée du son est également une caractéristique  (intuitive, cette dernière ne sera pas de ce fait détaillée dans les chapitres suivants).

-          le timbre est la  quatrième caractéristique d’un son  qui sera détaillée ci-après.

  

  

  

  

  

  

    Doc 3.1.a : Représentation graphique d’un son pur : une fonction sinusoïdale. On observe une périodicité flagrante avec une fréquence constante dans le temps. Un exemple de son presque pur est celui du diapason, en effet un son pur est introuvable dans la nature.

 

Le son complexe résulte généralement quant à lui de la superposition d’une multitude de sons purs. Ainsi on interprète celle d’un signal complexe comme la somme d’une multitude de sinusoïdes. L’ensemble des sons ne vérifient pas cette théorie. Une note d’un instrument de musique tel que le piano est un son complexe répondant parfaitement à cette notion acoustique.

 

 Doc 3.1.b : Représentation graphique d’un signal complexe. La parole (ou bruit) est un exemple très concret de son complexe.

 

 

 

Ces trois termes permettent de  définir la même caractéristique du son. La période est en fait l’intervalle de temps constant d’un phénomène dit périodique se répétant successivement à l’identique. Sur le document 3.1.a la période est mise en évidence par la lettre P.  La période T (seconde) est l’inverse de la fréquence F (Hertz) :      T = 1/F

     La fréquence est alors le nombre de périodes en une seule seconde soit le nombre de fois qu’un phénomène périodique se reproduit par unité de temps. La période et la fréquence étant liées directement, la relation donnant la fréquence F (Hertz) en fonction de la période T (seconde) est : F = 1/T

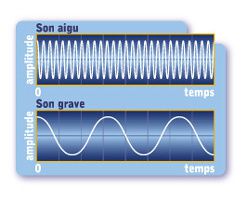
Plus la fréquence est élevée plus le son est aigu et plus elle est basse plus le son sera grave. Plus concrètement, le son grave d’un piano aura une plus faible fréquence que le son aigu de ce-dernier

Doc 3.1.1.a : Le son pur aigu représenté par la sinusoïde du haut a une fréquence élevée soit beaucoup de périodes en une seconde. A l’inverse le son pur grave représenté par la sinusoïde du bas a une fréquence faible soit très peu de périodes dans une unité de temps.

 

En acoustique musicale on parle plutôt de la hauteur du son mais elle est assimilée en physique à la fréquence. En effet, le diapason est l’outil du musicien donnant la hauteur de la « note  repère  conventionnelle » soit le La ayant une fréquence de 440 Hz, c’est la hauteur absolue du La 440 Hz.

Doc  3.1.1.b : Image d’un diapason  sur son socle donnant le son presque pur du La 440 Hz.

 

  

La fréquence d’un signal pur est facile à déterminer mais celle d’un son complexe l’est amplement moins. Comme dit précédemment, un son complexe  se compose d’une multitude de sinusoïdales. La fréquence de ce genre de signal est en fait caractérisée par la fréquence de son fondamentale. La fréquence fondamentale est l’harmonique de premier rang d’un son complexe. Quant à elles, les harmoniques se définissent par des fréquences étant des multiples entiers de la fréquence fondamentale. On peut donc dire qu’un son complexe est constitué d’une multitude de fréquences mais dont la première (fondamentale) le définie. Il existe une relation liant les harmoniques Fn (Hz),  la fréquence fondamentale Fo (Hz) et le rang des harmoniques noté n : Fn = n Fo

Le graphique ci-après (Doc 3.1.1.c) présente une analyse spectrale de l’amplitude de chaque harmonique d’un La 440 Hz.  Ce signal a une fréquence fondamentale (harmonique 1)  de 440 hertz (le La 440 Hz du piano) et voici ses 4 autres premières harmoniques multiples de la fondamentale :
- harmonique 2 : 880 Hz
- harmonique 3 : 1320 Hz
- harmonique 4 : 1760 Hz
- harmonique 5 : 2200 Hz
On distingue des harmoniques paires et impaires. Cette analyse spectrale illustre bien la relation donnée précédemment : soit la fréquence fondamentale  Fo = 440 Hz  et l’harmonique de rang n = 2, ainsi F2 = 2 x 440 <=> F2 = 880 Hz

 

 

Doc 3.1.1.c : Analyse spectrale d’un La 440 Hz

 

Le document (Doc 3.1.1.d) ci-après illustre le cas d’un signal complexe qui est la somme de plusieurs sinusoïdales étant les différentes harmoniques. Ici il n’y en a que trois qui apparaissent dont la fréquence fondamentale est 50 Hz.

 

 

Doc 3.1.1.d : Cas du son complexe

 

La longueur d’onde est une grandeur physique qui en général est la plus courte distance en mètre (m) entre deux points strictement identiques (en phase) d’une onde périodique. Dans le cas de l’onde sonore pure,  la longueur d’onde est en fait la distance la plus courte qui sépare deux points de deux tranches d’air distinctes dans le même état de compression.

 

 

Doc  3.1.2: Ce graphique représente la distance la plus courte en mètre entre deux points en position identique d’une sinusoïde telle que l’onde sonore : c’est la longueur d’onde notée λ et exprimée en mètre.

 

L’amplitude :

Le graphique 3.1.3.a ci-après représente une onde sinusoïdale et ses caractéristiques : cas par exemple d’un son pur.  Dans ce cas, l’amplitude peut être assimilée au niveau de compression (niveau de pression) des tranches d’air traversées par l’onde sonore. L’amplitude est directement liée au niveau sonore ou à l’intensité sonore.

On observe sur ce document les différentes amplitudes existantes et mesurables :
           - l'amplitude moyenne (la valeur moyenne arithmétique du signal positif)
           - l'amplitude efficace (amplitude continue équivalente en puissance)
           - l'amplitude (maximale positive)
           - l'amplitude crête à crête (l'écart maximal d'amplitude positive et négative)

 

 

Doc 3.1.3.a : schéma simplifié d’une onde sinusoïdale et de ses principales caractéristiques : période, longueur d’onde et amplitude

 

 

Le document 3.1.3.b représente plusieurs sinusoïdes  représentatives, par exemple, de plusieurs sons ayant chacun des amplitudes différentes. La courbe bleue a l’amplitude la plus importante tandis que la rouge a l’amplitude la plus faible. En effet, plus l’écart entre les deux crêtes est important et plus l’amplitude est grande.

 

 

 Doc 3.1.3.b : différents son purs d’amplitudes variées

 

L’intensité sonore:

L’onde sonore est, comme on l’a vu précédemment, caractérisée par des variations de pression du matériau dans lequel elle se propage. Ces variations de pression se traduisent sur une surface donnée du matériau considéré par des efforts mécaniques (forces de pression) dont la puissance mécanique est usuellement exprimée en Watts (W).

L’intensité sonore noté I est alors exprimée en Watt par mètre carré (w/m²). C’est donc la valeur caractérisant la puissance de l’onde P (W) transférée par l’onde à travers une surface S (m²). Ainsi il existe la relation suivante : I = P/S      

L’intensité sonore de référence notée Io est une valeur de référence intervenant dans la relation permettant de déterminer le niveau sonore L. Cette intensité  correspond au seuil d’audition d’un auditeur moyen qui est de l’ordre de 0 décibel pour un son sinusoïdale de fréquence 1000 Hz. On a donc Io = 10^-12 W.m^-2   

 

Le niveau sonore:

 

Le niveau sonore est une caractéristique de l’onde sonore correspondant au volume en musique mais encore à l’amplitude graphiquement. Par vulgarisation elle permet de distinguer un son fort et un son faible. Matériellement le niveau sonore correspond à l’écart de pression entre une couche d’air plus comprimée et une autre plus dilatée. Afin de déterminer le niveau sonore on utilise une échelle logarithmique, le choix d’un logarithme se justifie par le fait que cette approche reflète au mieux la sensation sonore de l’oreille humaine. La relation logarithmique permettant de calculer le niveau sonore L exprimé en décibel (dB) met en corrélation les intensités I du son et l’intensité Io de référence exprimée en Watt par mètre carré (W.m-2), on a donc : L = 10Log I/Io      

Par étude de cette relation on remarque que si l’on double l’intensité sonore I alors le niveau sonore  augmente de 3 décibels. Sur le même principe si l’on quadruple cette intensité le niveau sonore augmente de  6 dB..

Preuve : On a L’ = 10Log(2I/Io )= 10[log2 + logI/Io]

Ainsi L’ = 10log2+L ≈  L + 3    è Il y a donc une augmentation de 3 décibels si l’on multiplie l’intensité I par 2  N .B : log (axb) = log(a) + log(b)

Réciproquement si l’on augmente de 3 dB alors l’intensité sonore est doublée. Ainsi si un son à un niveau sonore de 110 dB et un autre de 120 dB alors le son de 120 dB a une intensité sonore environ 8 fois supérieur à l’autre, il est donc 8 fois plus « bruyant ». Pour autre exemple, une augmentation de 100 dB correspondant à une multiplication de l’intensité sonore de l’ordre du facteur 10 milliards.

De plus les niveaux sonores de plusieurs sons de s’ajoutent pas. Si l’on a deux sons d’intensités sonores I1 et I2  et de niveaux sonores L1= 10log I1/Io et L2 = 10log I2/Io, alors le niveau sonore L issue de la superposition des deux sons est L =  10 log (I1 + I2) / Io. On en déduit alors que L ≠ L1 + L2.

                                       

 

 

 

          Le timbre est également l’une des caractéristiques du son mais sur le plan acoustique c’est une notion très complexe. Il permet de distinguer deux sons musicaux (ou sons complexes) de même hauteur, de même durée et de même intensité (amplitude). Il permet également à une personne de reconnaître une voix qui lui est familière. Le timbre est d’une certaine façon la forme du son émis.

En effet à l’écoute de deux notes identiques (même intensité, hauteur et durée) émises par des instruments différents comme une guitare et une trompette, nous percevons  deux sons différents pour chacune des notes respectives des instruments. Cette différence entre les deux notes, pourtant identiques, s’explique par la notion de timbre.

         Le timbre varie selon plusieurs facteurs. Les intensités respectives (ou amplitudes relatives) de chaque harmonique composant un son complexe influent largement la caractérisation du timbre. En effet le timbre dépend de la corrélation entre la fréquence fondamentale, ses harmoniques et de leur intensité respective. 

De plus le timbre dépend également des régimes transitoires d’attaque et d’extinction du son. Ces phénomènes transitoires correspondent,

-          d’une part, à l’établissement de la note soit  aux premières millisecondes d’un son,

-          et d’autre part, à la phase finale du son soit aux dernières millisecondes de la note.

Dans le domaine musical par exemple, l’attaque d’un son est essentielle afin de déterminer son timbre et c’est donc l’attaque qui permet  de différencier deux façons de jouer une même note sur un même instrument. Ainsi,  si l’on supprime les 50 premières millisecondes des sons correspondants on  peut éventuellement ne plus en reconnaître le timbre et les différencier.

Le timbre varie aussi selon l’instrument de musique ou de la source sonore  utilisée mais également de la façon dont le musicien joue. L’analyse spectrale (Doc 3.1.1.c) permet de mettre en évidence la disposition des harmoniques et leurs amplitudes respectives, ceci permet l’étude du timbre d’un son.

Les  graphiques du Doc 3.1.4.a  représentent deux notes identiques : l’une jouée à la guitare (à gauche) et l’autre à la trompette (à droite).  L’amplitude est donnée en ordonnée et le temps en abscisse, malgré l’échelle différente on observe parfaitement que les deux sons ont la même fréquence fondamentale (ou hauteur), la même intensité (ou amplitude)  et la même durée. La forme respective de chaque courbe est par contre  différente, c’est alors le timbre des deux sons qui sont distincts. Ces variations de timbre entre les deux  notes pourtant les  mêmes sont observables d’une part par la forme général de chaque courbe. Cette différence de courbe dans chaque cas implique une disposition des harmoniques différente ainsi que des intensités relatives de chaque harmonique n’étant pas les mêmes, on pourrait d’ailleurs très bien le voir sur une analyse spectrale. Le timbre de chaque son diffère également à cause des régimes transitoires d’attaque et d’extinction qui sont totalement différents pour les deux sons.

 

 

 

Doc  3.1.4 : le timbre d’une guitare et d’une trompette.